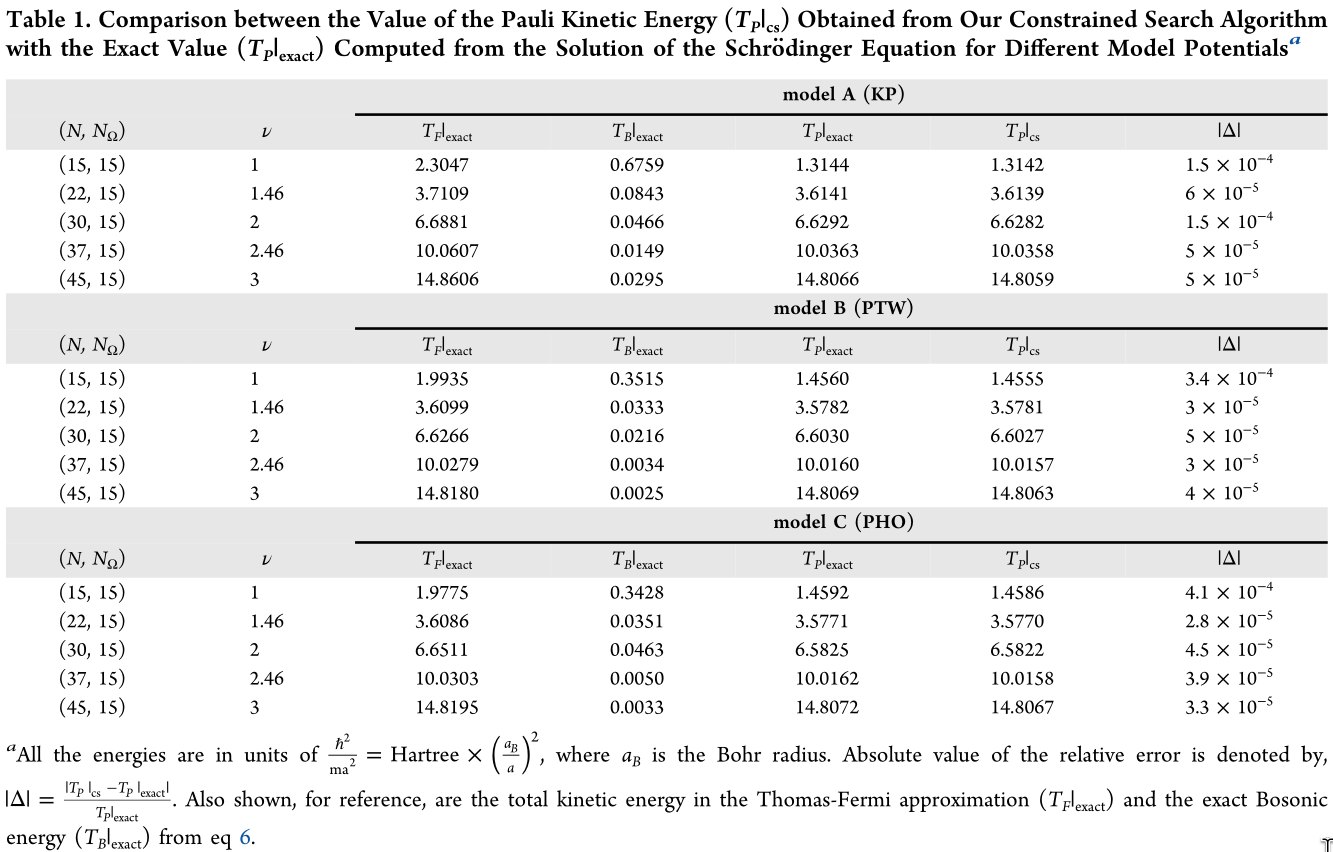
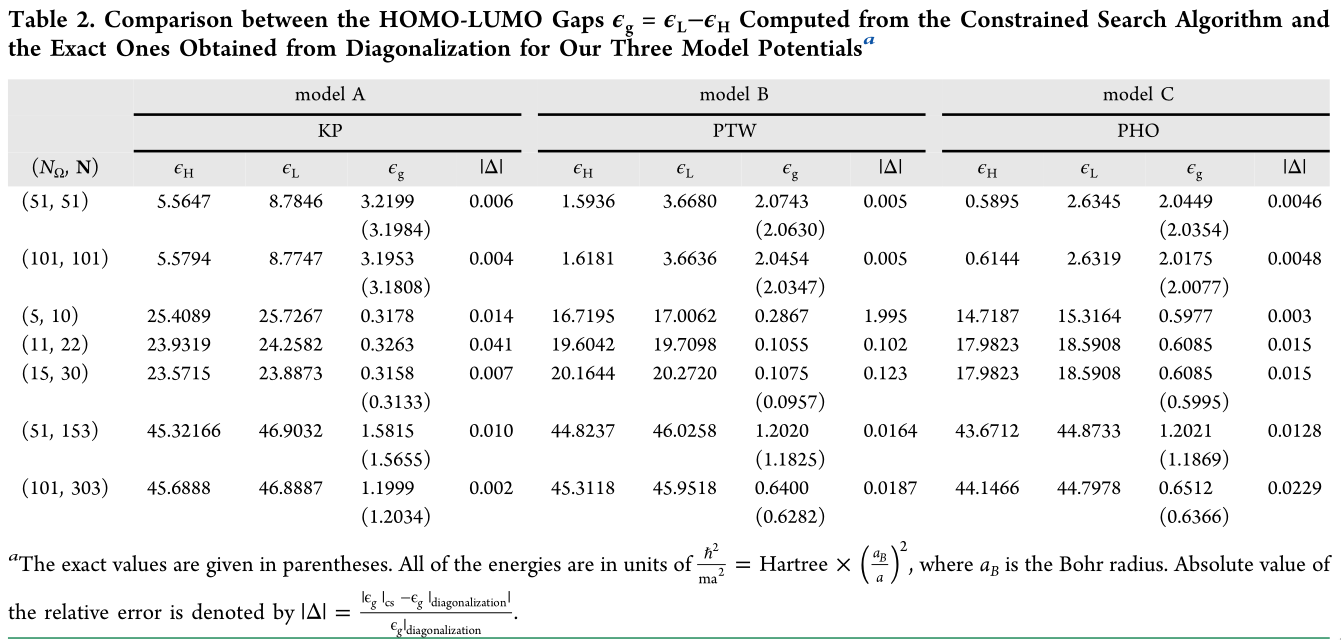
We present (1) a constrained search method for the noninteracting kinetic energy functional \(T_s[n]\) for periodic densities, which has analytical functional derivative \(V_s[n]\) at fixed electron number; (2) a routine for the derivative discontinuity—the uniform shift in \(V_s[n]\) upon changing particle number—thereby diagnosing noninteracting insulators vs conductors. The method uses the equidensity orbital (EO) basis and QR-based Stiefel manifold retraction. Benchmarks on 1D periodic systems reach chemical accuracy, indicating a viable path toward orbital-free treatments of periodic materials and novel way to invert periodic densities to obtain the Pauli potential for practical systems.
The noninteracting kinetic energy functional \(T_s[n]\)
Hohenberg-Kohn variational principle:
\[
E_0 = \min_n \left\{ F[n] + \int n(\vb{r}) V(\vb{r}) d\vb{r} \right\}
\]
the universal functional \(F[n]\) is defined as
\[
F[n] = \min_{\Psi\to n} \expval{\hat{T} + \hat{U}}{\Psi}
\]
The two-body interaction energy operator \(\hat{U}\) makes this computationally challenging.
Kohn-Sham formulation alleviates this by using an auxiliary noninteracting system where \(F[n]\) is split as:
\[
F[n] = T_s[n] + E_{Hxc}[n]
\]
where the noninteracting kinetic energy $T_s[n]$ is given by solution of the constrained search
\[
T_s[n] = \min_{\Psi\to n} \expval{\hat{T}}{\Psi}.
\]
The stationary condition of the Lagrangian associated with the Kohn-Sham variational principle gives the relation
\[
\fdv{T_s[n]}{n} = -V_s(\vb{r}) = -\fdv{E_{Hxc}[n]}{n} - V(\vb{r}).
\]
Therefore the density inversion problem that solves for the Kohn-Sham potential \(V_s[n]\) for a given prescribed
density $n$ can be solved by taking the functional derivative of $T_s[n]$.

The bosonic functional
\[
T_B[n] = \int \frac{\abs{\nabla n(\vb{r })}^2}{8 n(\vb{r})} d\vb{r}
\]
gives the kinetic energy of a system of noninteracting bosons in the ground state with density $n(r)$, so one
can define the remaining part of $T_s[n]$ that arises from the Pauli exclusion principle as the Pauli kinetic
energy functional $T_P[n]\equiv T_s[n]-T_B[n]$. Since the Bosonic potential is known analytically
\[
V_B(\vb{r}) = \fdv{T_B[n]}{n} = -\frac{\nabla^2 \sqrt{n(\vb{r})}}{4 \sqrt{n(\vb{r})}},
\]
solving for the Pauli potential $V_P(\vb{r})=\fdv{T_P[n]}{n}$ is equivalent to solving for \(V_s[n]\), i.e.
performing density inversion.
If analytical expressions for \(T_s[n]\) were known, the Kohn-Sham equations could be solved directly without the need for orbitals either by directly searching over $n$ integrating to the number of electrons $N$ that gives the minimal energy, or by solving the following bosonic problem after density inversion
\[
\left\{ - \frac{1}{2} + V_P[n] + V_s[n] - \mu \right\} \sqrt{n(\vb{r})} = 0.
\]
This is the goal of orbital-free DFT.
However, there are no known analytical expressions for the $T_s[n]$.
Consider a periodic system with a cubic unit cell of size $a$, where the FBZ is discretized by employing PBC over a
supercell $\mathcal{B}$ with $N_\Omega$ unit cells.
Given a prescribed density $n(\vb{r})$ that integrates to $N=\sum_{\vb{k}\in \text{BZ}}N_{\vb{k}}$, EOs are defined
as
\[
\phi_{\vb{k}+\vb{G}}(\vb{r}) = \sqrt{\frac{n(\vb{r})}{N}} e^{\vb{i} (\vb{k}+\vb{G}) \cdot \vb*{\xi}(\vb{r})}
\]
where $\vb{G}$ are reciprocal vectors on the lattice and $\vb*{\xi}:\mathcal{B}\to\mathcal{B}$ is the solution to
the Jacobian problem
\[
\det \left( \pdv{\xi_i(\vb{r})}{r_j} \right) = \frac{n(\vb{r})}{N}.
\]
EOs form a complete orthonormal basis and has the same density as $n(\vb{r})$.
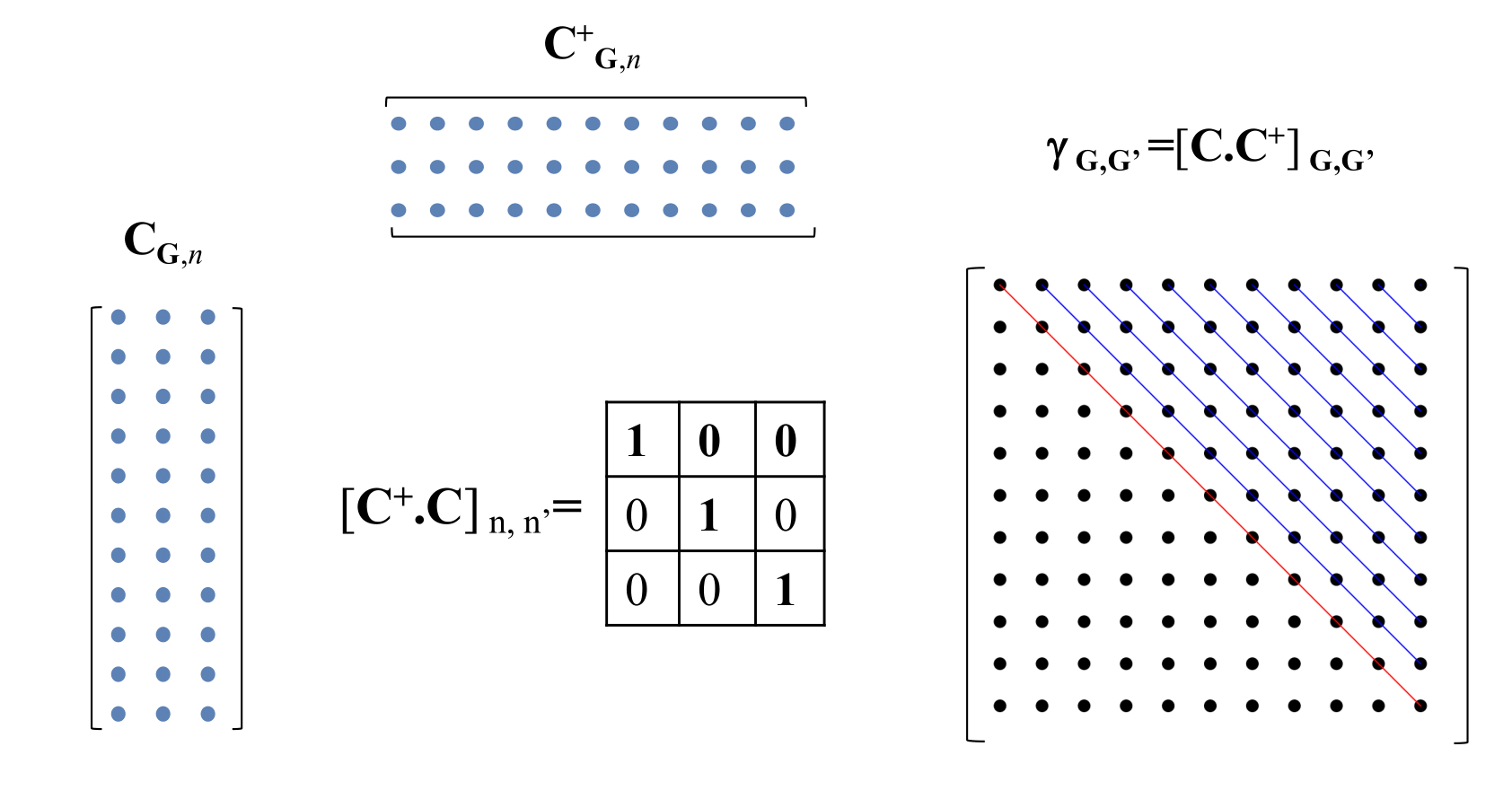
Orthonormal orbitals under this basis
$\ket{\varphi_{\vb{k}}}=\sum_{\vb{G}}C(\vb{k})_{\vb{G}}\ket{\phi_{\vb{k}+\vb{G}}}$ also has density $n(\vb{r})$ if
the "subtraces" constraint
\[
g_{\vb{Q}}(\vb{C}) = \sum_{\vb{k}\in \text{BZ},\vb{G}} \gamma(\vb{k})_{\vb{G}, \vb{G+Q}} = N\delta_{\vb{Q}, 0}
\]
is satisfied where $\gamma(\vb{k})_{\vb{G}, \vb{G}'}=[C(\vb{k}) \cdot C^\dagger(\vb{k})]_{\vb{G}, \vb{G}'}$ is the
one-particle density matrix in EO basis at $\vb{k}$.
Under this constraint, we further have
\[
T_{P}[n] = \frac{1}{8N} \int d\vb{r}\; n(\vb{r}) \sum_{\vb{G}, \vb{G}'} \gamma(\vb{k})_{\vb{G}, \vb{G}'} e^{- \vb{i}
(\vb{G}'- \vb{G}) \cdot \vb*{\xi
}(\vb{r})} [ \grad_{\vb{r}} (\vb{k} + \vb{G} + \vb{G}') \cdot \vb*{\xi }(\vb{r})]^{2}
\]
We used QR-based retraction for the Stiefel manifold so the orthonormality $C(\vb{k})^\dagger C(\vb{k}) = I$ is
always satisfied. The subtrace constraint is enforced via the method of Modified Differential Multipliers Method
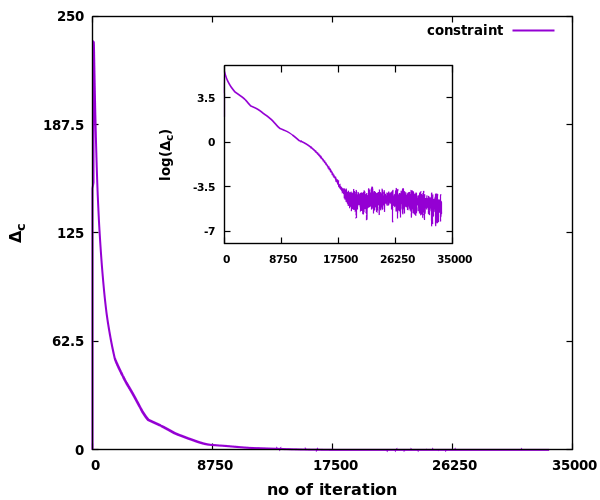
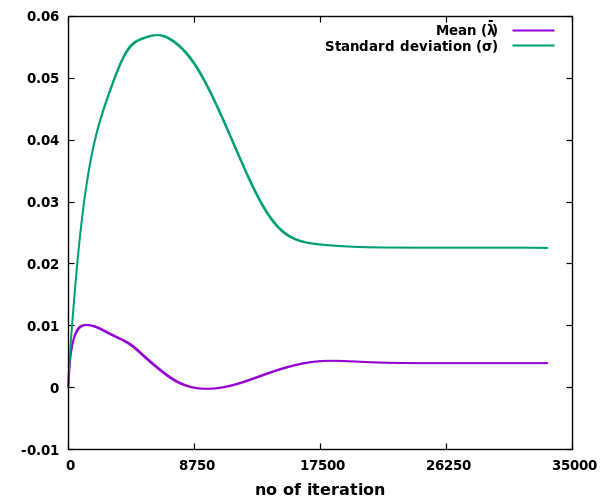
(MDMM), where the constraint is satisfied gradually over the optimization iterations.
We show that the \(T_s[n]\) computed with our methods satisfies exact scaling relation
\[
T_s[n_\lambda] = \lambda^{2} T_s[n], \quad n_\lambda(\vb{r}) = \lambda^d n(\lambda \vb{r}),
\]
References and web version

- S. Majumdar, Z. Shi, and G. Vignale J. Chem. Theory Comput.
21:6007-6022, 2025.
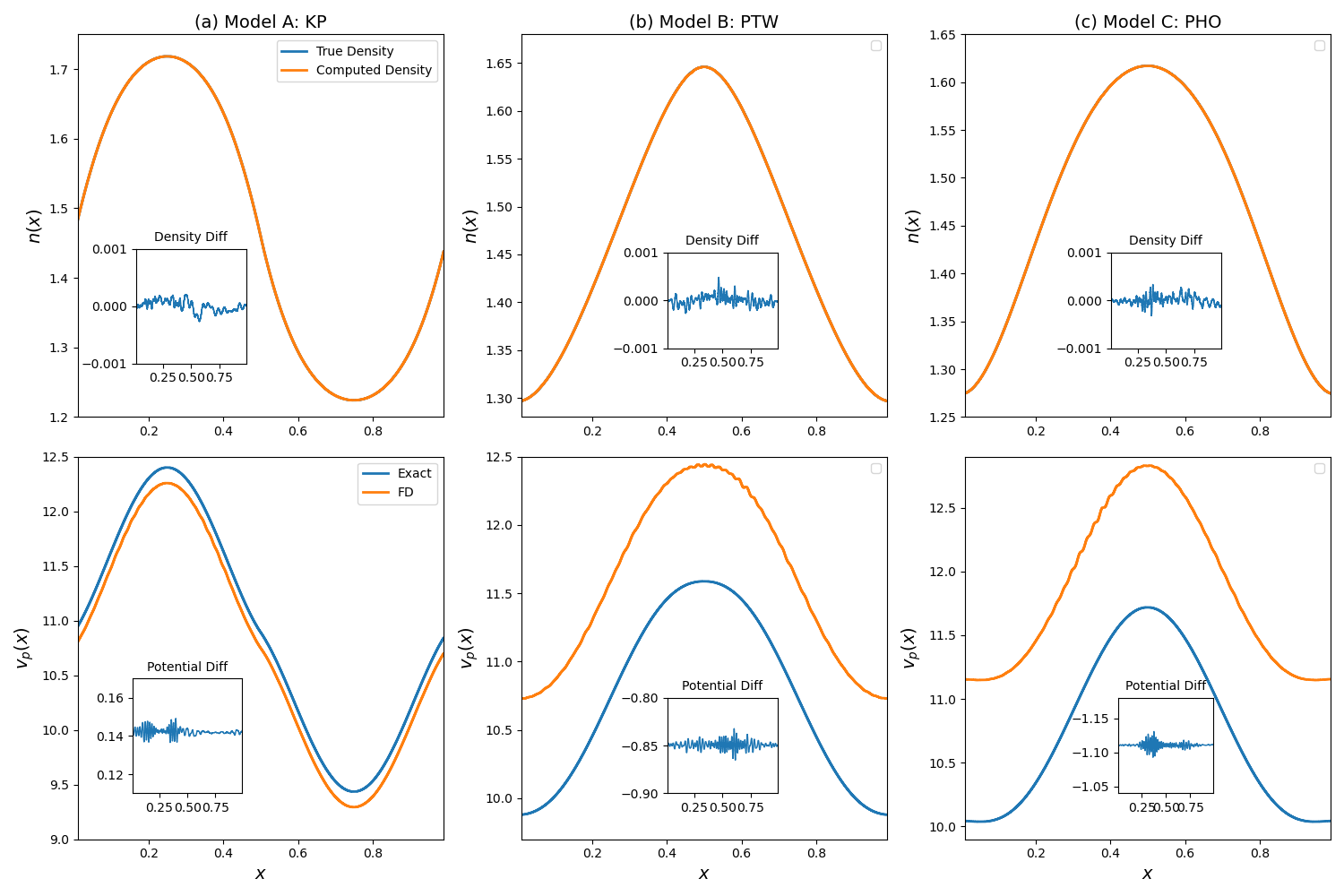
Inversion result on exactly solvable systems
The functional derivative $V_P[n]$ under the EO basis can be derived analytically from the expression of $T_P[n]$.
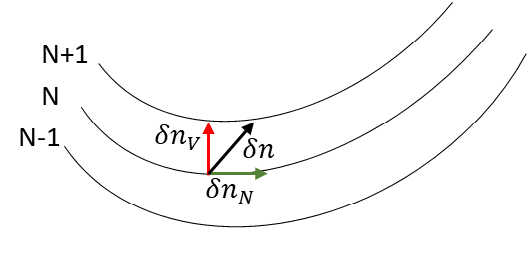
The constrained search finds the stationary point of the Lagrangian \(\mathcal{L}[n, \mu]=T_s[n]+ \mu (\int n(\vb{r}) d\vb{r}-N)\). Although we can compute the functional derivative at the stationary point analytically, $\mu$ introduces a gauge freedom to \(V_s[n]\), and the variation \(\delta n_N\) is tangential to the $N$-particle sheet \(\{n\mid \int n(\vb{r}) d\vb{r}=N \}\). We define a connection $\delta n_V$ that transport density from the $N$-particle sheet to the \(N\pm 1\)-particle sheet as
\[
\delta n_+(\vb{r}) = \frac{1}{N_\Omega} \abs{\Psi_L[n](\vb{r})}^2, \quad
\delta n_-(\vb{r}) = -\frac{1}{N_\Omega} \abs{\Psi_H[n](\vb{r})}^2,
\]
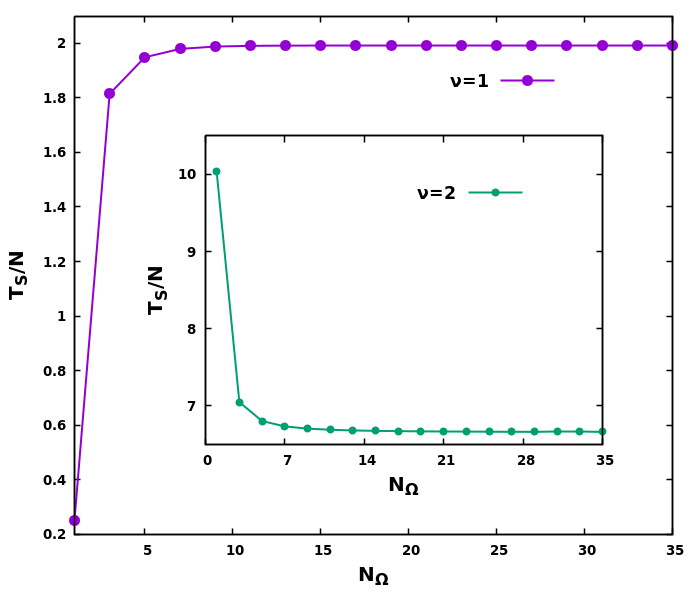
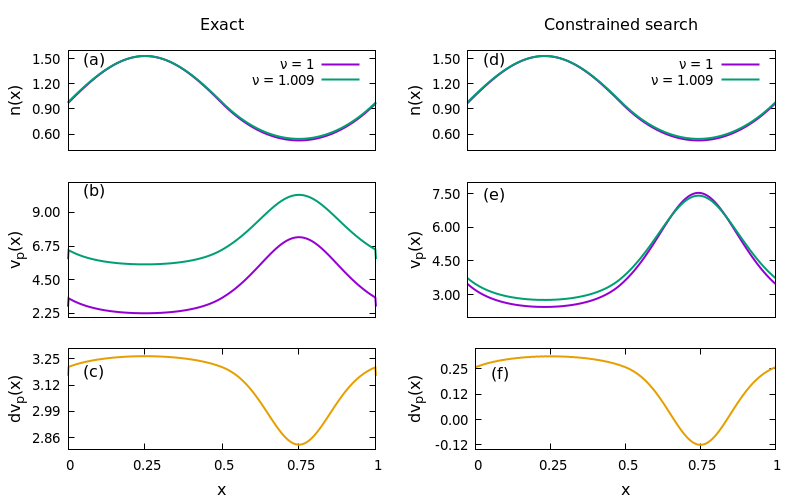
where $\Psi_L[n],\Psi_H[n]$ are LUMO and HOMO at density $n$. This effectively computes the functional derivative of $T_s[n]$ at fixed potential $V_s$. w.r.t. variable filling factor $\nu \equiv N / N_\Omega$, which is continuous when $N_\Omega\to \infty$.